Job Search V: Modeling Career Choice¶
In addition to what’s in Anaconda, this lecture will need the following libraries:
!conda install -y quantecon
import numpy as np
import quantecon as qe
import matplotlib.pyplot as plt
%matplotlib inline
from numba import njit, prange
from quantecon.distributions import BetaBinomial
from scipy.special import binom, beta
from mpl_toolkits.mplot3d.axes3d import Axes3D
from matplotlib import cm
Model Features¶
- Career and job within career both chosen to maximize expected discounted wage flow.
- Infinite horizon dynamic programming with two state variables.
Model¶
In what follows we distinguish between a career and a job, where
- a career is understood to be a general field encompassing many possible jobs, and
- a job is understood to be a position with a particular firm
For workers, wages can be decomposed into the contribution of job and career
- $ w_t = \theta_t + \epsilon_t $, where
- $ \theta_t $ is the contribution of career at time $ t $
- $ \epsilon_t $ is the contribution of the job at time $ t $
At the start of time $ t $, a worker has the following options
- retain a current (career, job) pair $ (\theta_t, \epsilon_t) $ — referred to hereafter as “stay put”
- retain a current career $ \theta_t $ but redraw a job $ \epsilon_t $ — referred to hereafter as “new job”
- redraw both a career $ \theta_t $ and a job $ \epsilon_t $ — referred to hereafter as “new life”
Draws of $ \theta $ and $ \epsilon $ are independent of each other and past values, with
- $ \theta_t \sim F $
- $ \epsilon_t \sim G $
Notice that the worker does not have the option to retain a job but redraw a career — starting a new career always requires starting a new job.
A young worker aims to maximize the expected sum of discounted wages
$$ \mathbb{E} \sum_{t=0}^{\infty} \beta^t w_t \tag{1} $$
subject to the choice restrictions specified above.
Let $ v(\theta, \epsilon) $ denote the value function, which is the maximum of (1) overall feasible (career, job) policies, given the initial state $ (\theta, \epsilon) $.
The value function obeys
$$ v(\theta, \epsilon) = \max\{I, II, III\} $$where
$$ \begin{aligned} & I = \theta + \epsilon + \beta v(\theta, \epsilon) \\ & II = \theta + \int \epsilon' G(d \epsilon') + \beta \int v(\theta, \epsilon') G(d \epsilon') \nonumber \\ & III = \int \theta' F(d \theta') + \int \epsilon' G(d \epsilon') + \beta \int \int v(\theta', \epsilon') G(d \epsilon') F(d \theta') \nonumber \end{aligned} \tag{2} $$
Evidently $ I $, $ II $ and $ III $ correspond to “stay put”, “new job” and “new life”, respectively.
Parameterization¶
As in [LS18], section 6.5, we will focus on a discrete version of the model, parameterized as follows:
- both $ \theta $ and $ \epsilon $ take values in the set
np.linspace(0, B, grid_size)— an even grid of points between $ 0 $ and $ B $ inclusive grid_size = 50B = 5β = 0.95
The distributions $ F $ and $ G $ are discrete distributions
generating draws from the grid points np.linspace(0, B, grid_size).
A very useful family of discrete distributions is the Beta-binomial family, with probability mass function
$$ p(k \,|\, n, a, b) = {n \choose k} \frac{B(k + a, n - k + b)}{B(a, b)}, \qquad k = 0, \ldots, n $$Interpretation:
- draw $ q $ from a Beta distribution with shape parameters $ (a, b) $
- run $ n $ independent binary trials, each with success probability $ q $
- $ p(k \,|\, n, a, b) $ is the probability of $ k $ successes in these $ n $ trials
Nice properties:
- very flexible class of distributions, including uniform, symmetric unimodal, etc.
- only three parameters
Here’s a figure showing the effect on the pmf of different shape parameters when $ n=50 $.
def gen_probs(n, a, b):
probs = np.zeros(n+1)
for k in range(n+1):
probs[k] = binom(n, k) * beta(k + a, n - k + b) / beta(a, b)
return probs
n = 50
a_vals = [0.5, 1, 100]
b_vals = [0.5, 1, 100]
fig, ax = plt.subplots(figsize=(10, 6))
for a, b in zip(a_vals, b_vals):
ab_label = f'$a = {a:.1f}$, $b = {b:.1f}$'
ax.plot(list(range(0, n+1)), gen_probs(n, a, b), '-o', label=ab_label)
ax.legend()
plt.show()
Implementation¶
We will first create a class CareerWorkerProblem which will hold the
default parameterizations of the model and an initial guess for the value function.
class CareerWorkerProblem:
def __init__(self,
B=5.0, # Upper bound
β=0.95, # Discount factor
grid_size=50, # Grid size
F_a=1,
F_b=1,
G_a=1,
G_b=1):
self.β, self.grid_size, self.B = β, grid_size, B
self.θ = np.linspace(0, B, grid_size) # Set of θ values
self.ϵ = np.linspace(0, B, grid_size) # Set of ϵ values
self.F_probs = BetaBinomial(grid_size - 1, F_a, F_b).pdf()
self.G_probs = BetaBinomial(grid_size - 1, G_a, G_b).pdf()
self.F_mean = np.sum(self.θ * self.F_probs)
self.G_mean = np.sum(self.ϵ * self.G_probs)
# Store these parameters for str and repr methods
self._F_a, self._F_b = F_a, F_b
self._G_a, self._G_b = G_a, G_b
The following function takes an instance of CareerWorkerProblem and returns
the corresponding Bellman operator $ T $ and the greedy policy function.
In this model, $ T $ is defined by $ Tv(\theta, \epsilon) = \max\{I, II, III\} $, where $ I $, $ II $ and $ III $ are as given in (2).
def operator_factory(cw, parallel_flag=True):
"""
Returns jitted versions of the Bellman operator and the
greedy policy function
cw is an instance of ``CareerWorkerProblem``
"""
θ, ϵ, β = cw.θ, cw.ϵ, cw.β
F_probs, G_probs = cw.F_probs, cw.G_probs
F_mean, G_mean = cw.F_mean, cw.G_mean
@njit(parallel=parallel_flag)
def T(v):
"The Bellman operator"
v_new = np.empty_like(v)
for i in prange(len(v)):
for j in prange(len(v)):
v1 = θ[i] + ϵ[j] + β * v[i, j] # Stay put
v2 = θ[i] + G_mean + β * v[i, :] @ G_probs # New job
v3 = G_mean + F_mean + β * F_probs @ v @ G_probs # New life
v_new[i, j] = max(v1, v2, v3)
return v_new
@njit
def get_greedy(v):
"Computes the v-greedy policy"
σ = np.empty(v.shape)
for i in range(len(v)):
for j in range(len(v)):
v1 = θ[i] + ϵ[j] + β * v[i, j]
v2 = θ[i] + G_mean + β * v[i, :] @ G_probs
v3 = G_mean + F_mean + β * F_probs @ v @ G_probs
if v1 > max(v2, v3):
action = 1
elif v2 > max(v1, v3):
action = 2
else:
action = 3
σ[i, j] = action
return σ
return T, get_greedy
Lastly, solve_model will take an instance of CareerWorkerProblem and
iterate using the Bellman operator to find the fixed point of the value function.
def solve_model(cw,
use_parallel=True,
tol=1e-4,
max_iter=1000,
verbose=True,
print_skip=25):
T, _ = operator_factory(cw, parallel_flag=use_parallel)
# Set up loop
v = np.ones((cw.grid_size, cw.grid_size)) * 100 # Initial guess
i = 0
error = tol + 1
while i < max_iter and error > tol:
v_new = T(v)
error = np.max(np.abs(v - v_new))
i += 1
if verbose and i % print_skip == 0:
print(f"Error at iteration {i} is {error}.")
v = v_new
if i == max_iter:
print("Failed to converge!")
if verbose and i < max_iter:
print(f"\nConverged in {i} iterations.")
return v_new
Here’s the solution to the model – an approximate value function
cw = CareerWorkerProblem()
T, get_greedy = operator_factory(cw)
v_star = solve_model(cw, verbose=False)
greedy_star = get_greedy(v_star)
fig = plt.figure(figsize=(8, 6))
ax = fig.add_subplot(111, projection='3d')
tg, eg = np.meshgrid(cw.θ, cw.ϵ)
ax.plot_surface(tg,
eg,
v_star.T,
cmap=cm.jet,
alpha=0.5,
linewidth=0.25)
ax.set(xlabel='θ', ylabel='ϵ', zlim=(150, 200))
ax.view_init(ax.elev, 225)
plt.show()
And here is the optimal policy
fig, ax = plt.subplots(figsize=(6, 6))
tg, eg = np.meshgrid(cw.θ, cw.ϵ)
lvls = (0.5, 1.5, 2.5, 3.5)
ax.contourf(tg, eg, greedy_star.T, levels=lvls, cmap=cm.winter, alpha=0.5)
ax.contour(tg, eg, greedy_star.T, colors='k', levels=lvls, linewidths=2)
ax.set(xlabel='θ', ylabel='ϵ')
ax.text(1.8, 2.5, 'new life', fontsize=14)
ax.text(4.5, 2.5, 'new job', fontsize=14, rotation='vertical')
ax.text(4.0, 4.5, 'stay put', fontsize=14)
plt.show()
Interpretation:
- If both job and career are poor or mediocre, the worker will experiment with a new job and new career.
- If career is sufficiently good, the worker will hold it and experiment with new jobs until a sufficiently good one is found.
- If both job and career are good, the worker will stay put.
Notice that the worker will always hold on to a sufficiently good career, but not necessarily hold on to even the best paying job.
The reason is that high lifetime wages require both variables to be large, and the worker cannot change careers without changing jobs.
- Sometimes a good job must be sacrificed in order to change to a better career.
Exercises¶
Exercise 1¶
Using the default parameterization in the class CareerWorkerProblem,
generate and plot typical sample paths for $ \theta $ and $ \epsilon $
when the worker follows the optimal policy.
In particular, modulo randomness, reproduce the following figure (where the horizontal axis represents time)
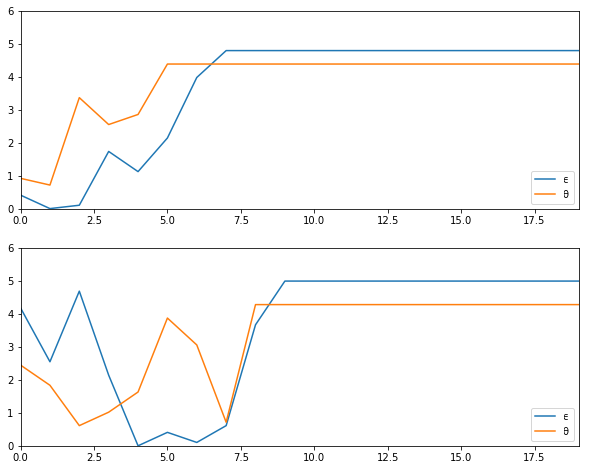
Hint: To generate the draws from the distributions $ F $ and $ G $, use quantecon.random.draw().
Exercise 2¶
Let’s now consider how long it takes for the worker to settle down to a permanent job, given a starting point of $ (\theta, \epsilon) = (0, 0) $.
In other words, we want to study the distribution of the random variable
$$ T^* := \text{the first point in time from which the worker's job no longer changes} $$Evidently, the worker’s job becomes permanent if and only if $ (\theta_t, \epsilon_t) $ enters the “stay put” region of $ (\theta, \epsilon) $ space.
Letting $ S $ denote this region, $ T^* $ can be expressed as the first passage time to $ S $ under the optimal policy:
$$ T^* := \inf\{t \geq 0 \,|\, (\theta_t, \epsilon_t) \in S\} $$Collect 25,000 draws of this random variable and compute the median (which should be about 7).
Repeat the exercise with $ \beta=0.99 $ and interpret the change.
Exercise 3¶
Set the parameterization to G_a = G_b = 100 and generate a new optimal policy
figure – interpret.
Solutions¶
Exercise 1¶
Simulate job/career paths.
In reading the code, recall that optimal_policy[i, j] = policy at
$ (\theta_i, \epsilon_j) $ = either 1, 2 or 3; meaning ‘stay put’,
‘new job’ and ‘new life’.
F = np.cumsum(cw.F_probs)
G = np.cumsum(cw.G_probs)
v_star = solve_model(cw, verbose=False)
T, get_greedy = operator_factory(cw)
greedy_star = get_greedy(v_star)
def gen_path(optimal_policy, F, G, t=20):
i = j = 0
θ_index = []
ϵ_index = []
for t in range(t):
if greedy_star[i, j] == 1: # Stay put
pass
elif greedy_star[i, j] == 2: # New job
j = int(qe.random.draw(G))
else: # New life
i, j = int(qe.random.draw(F)), int(qe.random.draw(G))
θ_index.append(i)
ϵ_index.append(j)
return cw.θ[θ_index], cw.ϵ[ϵ_index]
fig, axes = plt.subplots(2, 1, figsize=(10, 8))
for ax in axes:
θ_path, ϵ_path = gen_path(greedy_star, F, G)
ax.plot(ϵ_path, label='ϵ')
ax.plot(θ_path, label='θ')
ax.set_ylim(0, 6)
plt.legend()
plt.show()
Exercise 2¶
The median for the original parameterization can be computed as follows
cw = CareerWorkerProblem()
F = np.cumsum(cw.F_probs)
G = np.cumsum(cw.G_probs)
T, get_greedy = operator_factory(cw)
v_star = solve_model(cw, verbose=False)
greedy_star = get_greedy(v_star)
@njit
def passage_time(optimal_policy, F, G):
t = 0
i = j = 0
while True:
if optimal_policy[i, j] == 1: # Stay put
return t
elif optimal_policy[i, j] == 2: # New job
j = int(qe.random.draw(G))
else: # New life
i, j = int(qe.random.draw(F)), int(qe.random.draw(G))
t += 1
@njit(parallel=True)
def median_time(optimal_policy, F, G, M=25000):
samples = np.empty(M)
for i in prange(M):
samples[i] = passage_time(optimal_policy, F, G)
return np.median(samples)
median_time(greedy_star, F, G)
To compute the median with $ \beta=0.99 $ instead of the default
value $ \beta=0.95 $, replace cw = CareerWorkerProblem() with
cw = CareerWorkerProblem(β=0.99).
The medians are subject to randomness but should be about 7 and 14 respectively.
Not surprisingly, more patient workers will wait longer to settle down to their final job.
Exercise 3¶
cw = CareerWorkerProblem(G_a=100, G_b=100)
T, get_greedy = operator_factory(cw)
v_star = solve_model(cw, verbose=False)
greedy_star = get_greedy(v_star)
fig, ax = plt.subplots(figsize=(6, 6))
tg, eg = np.meshgrid(cw.θ, cw.ϵ)
lvls = (0.5, 1.5, 2.5, 3.5)
ax.contourf(tg, eg, greedy_star.T, levels=lvls, cmap=cm.winter, alpha=0.5)
ax.contour(tg, eg, greedy_star.T, colors='k', levels=lvls, linewidths=2)
ax.set(xlabel='θ', ylabel='ϵ')
ax.text(1.8, 2.5, 'new life', fontsize=14)
ax.text(4.5, 2.5, 'new job', fontsize=14, rotation='vertical')
ax.text(4.0, 4.5, 'stay put', fontsize=14)
plt.show()
In the new figure, you see that the region for which the worker stays put has grown because the distribution for $ \epsilon $ has become more concentrated around the mean, making high-paying jobs less realistic.
